Simplified explanation of how RSA message encryption/decryption works

Introduction

After making a small DES illustration I wanted to create similar thing but for AES. After some consideration I decided not to do it as it was very similar and decided to go with RSA because I really liked it on first encounter with the algorithm. From all the algorithms used in SSL it felt like RSA is the simplest and most elegant one. I will try to show it’s simplicity.

For total beginners RSA is an alorithm to securely share information from one person to another over insecure medium. To do so we need to encrypt information so that evesdropping third parties cannot “read” original message. In this post I want to focus only on message encryption and decryption and will fully ignore algorithm of key generation.

RSA algorithm

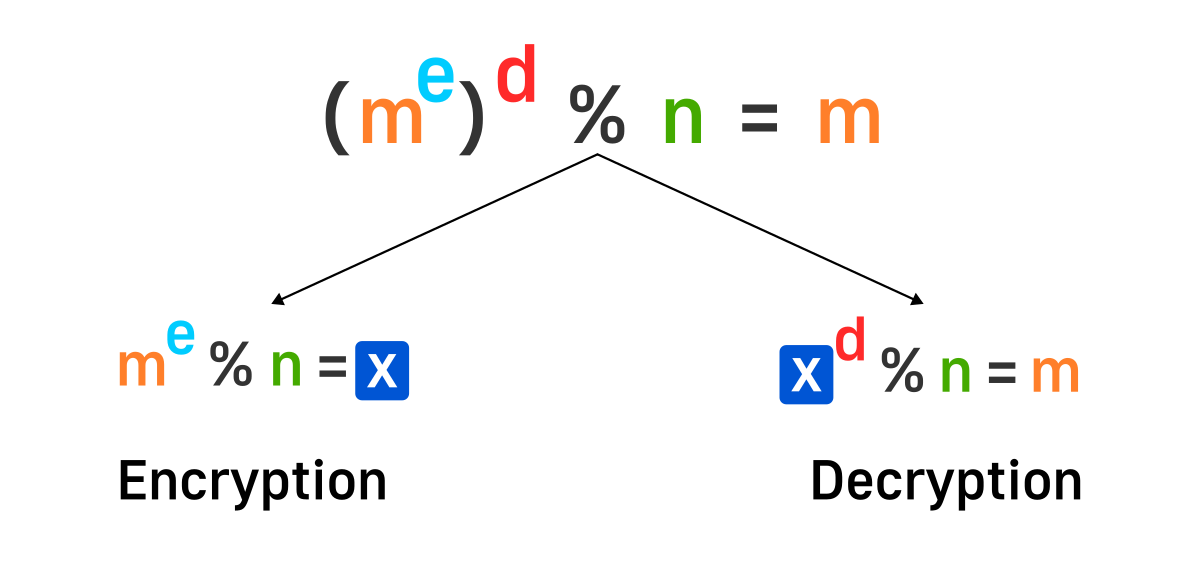
RSA is very simple and elegant. It is just a “simple” math formula which looks like this:

Here m is our message represented as a single number. e, d, and n are three positivite integers specially selected to satisfy the equation above.

m = message
e and n = public key
d = private key
n = modulus

The smallest number combination that suits this equation is e=3, d=3 and n=15 (if we decide not to allow exponents of value 1). Since 15 is our modulus it means that we can send number from 1 up to 15 as any number modulus 15 will give us numbers in that range.

1**9 % 15  = 1     or    (1**3 % 15)**3 % 15 = 1
2**9 % 15  = 2     or    (2**3 % 15)**3 % 15 = 2
3**9 % 15  = 3     or    (3**3 % 15)**3 % 15 = 3
4**9 % 15  = 4     or    (4**3 % 15)**3 % 15 = 4
5**9 % 15  = 5     or    (5**3 % 15)**3 % 15 = 5
6**9 % 15  = 6     or    (6**3 % 15)**3 % 15 = 6
7**9 % 15  = 7     or    (7**3 % 15)**3 % 15 = 7
8**9 % 15  = 8     or    (8**3 % 15)**3 % 15 = 8
9**9 % 15  = 9     or    (9**3 % 15)**3 % 15 = 9
10**9 % 15 = 10    or    (10**3 % 15)**3 % 15 = 10
11**9 % 15 = 11    or    (11**3 % 15)**3 % 15 = 11
12**9 % 15 = 12    or    (12**3 % 15)**3 % 15 = 12
13**9 % 15 = 13    or    (13**3 % 15)**3 % 15 = 13
14**9 % 15 = 14    or    (14**3 % 15)**3 % 15 = 14

Because of distribute property of modululo operation we can expand our equation by splitting our exponenent into two parts each with its own exponent. At the beginning we chose both of our exponents to be 3.

So with this we can say that 3 and 15 is our public key and tell it to other people who want to communicate with us. Let’s say some person want to send us number 12. To do that they will have to do 12**3%15 = 3 and send us number 3. In this case 3 is encrypted message and when sent over the network will not expose initial number of 12. On our end when we receive number encrypted number we just do 3**3%15 = 12.

Sending text

What if we want to send some text instead of a number 12? It is easy. First we need to convert our text to numeric representation. One way to do it is to encode with message with ascii table or unicode. Since unicode and ascii overlap for enlish text let’s go for ascii for now. Let’s say we want to send message ‘Hello world!’ over the wire with RSA. Here are values for each letter in their numeric form, both in decimal and hex formats.

'H'  72   0x48
'e'  101  0x65
'l'  108  0x6c
'l'  108  0x6c
'o'  111  0x6f
' '  32   0x20
'w'  119  0x77
'o'  111  0x6f
'r'  114  0x72
'l'  108  0x6c
'd'  100  0x64
'!'  33   0x21

Then we just concatenate all the number values one after another (big endian?) and get just a very big number 0x48656c6c6f20776f726c6421 or in decimal 22405534230753963835153736737. But this time our modulus 15 will not work. We need a modulus that is larger than the message that we are trying to send or in other words larger than 22405534230753963835153736737. I will be using hexadecimal representation of number because they more easily translate to bytes. So if we want to send this message we need a modulus that is at least 12 bytes (number of digits in 0x48656c6c6f20776f726c6421 is 24 and each digit is half byte, so 12 bytes) or 96 bits.

For this to work I will use these selected numbers:

d: 19561913760612153243824779553
e: 65537
n: 41780320747247905576602646597

e or public exponent is mostly 65537 or 0x010001 in hex. Selected modulus is 41780320747247905576602646597. So to encrypt our message we exponentiate and take modulus: 22405534230753963835153736737 ** 65537 % 41780320747247905576602646597 = 9677577356176148501889172774. So this big number 9677577356176148501889172774 is the number you would need to send to the another party as encrypted message. Also note at the amount of computation you have to do here. You take 22405534230753963835153736737 and multiple it 65536 time by itself. Quite a lot of multiplications.

On receving party will receive a number 9677577356176148501889172774 as encrypted message and will have to do similar computation but with different exponent or: 9677577356176148501889172774 ** 19561913760612153243824779553 % 41780320747247905576602646597 = 22405534230753963835153736737. Here if you had to use exponent of 65537 for encryption, the other person will use 19561913760612153243824779553 exponent to decrypt. This computation is a lot lot more. For encryption you can use python and just replicate it for decryption unfortunately it will take quite a lot of time. I tried on my computer and gave up. For that I used some of my own tools with some tricks to speed up calculations.

So as a result we got a number 22405534230753963835153736737 or 0x48656c6c6f20776f726c6421. If you look the table with character above you will see that it is exactly the same combination: 0x48 = H, 0x65 = e and etc. So we got our ‘Hello world!’ message.

Padding

Even though the above method work it has some security problems with replaing messages, small messages and etc. To tackle this issues messages padded before encrypting. There are different ways to pad message but let’s look at one of them PKCS#1.

In the example of sending text we used 96 bits to encrypt message. But in real world people don’t use such small keys. Today default key size is 2048 bits. For this example I will use 512 bits as it will take less space to show details.

So 512 bits is 64 bytes and our message (Hello world!) is 12 bytes. Selected padding format is like this: [0x00][0x02][random bytes][0x00][message]. The first byte is always 0. Second byte is 2 and specified what padding format we are using. Then we have a number of random bytes with a terminating 0 byte. After all that we end everything with our message that we want to send. So our message becomes: 0x0002rrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrr0048656c6c6f20776f726c6421, where r = random byte.

RFC 2313 advices to have 11 byte header which if we remove top 2 bytes and terminating 0 byte gives us at least 8 bytes of random bytes in each message. This is good as hackers won’t be able to send the same message multiple time in their replay attacks.

Generating exponents and modulus

In this post I will not be diving into topic of how to generate keys ourself as I don’t think it give much insigth into the discussion. This black box will remain closed and maybe we could look into it more in some other post. But I want to have a look at least at how to get those keys.

There are multiple way to generate keys and here I will look into openssl’s toolbox. Here is a command to generate private and public keys:

openssl req -nodes -new -x509 -keyout private.key -out public.cert

After filling some inforamtion it will create two files: private.key and public.cert. If you do any server management then you have seen different variations of these files on your server when you were setting up nginx or something similar. There are simpler ways to generate exponents but I wanted to do it this way to make it closer to our day to day usecases.

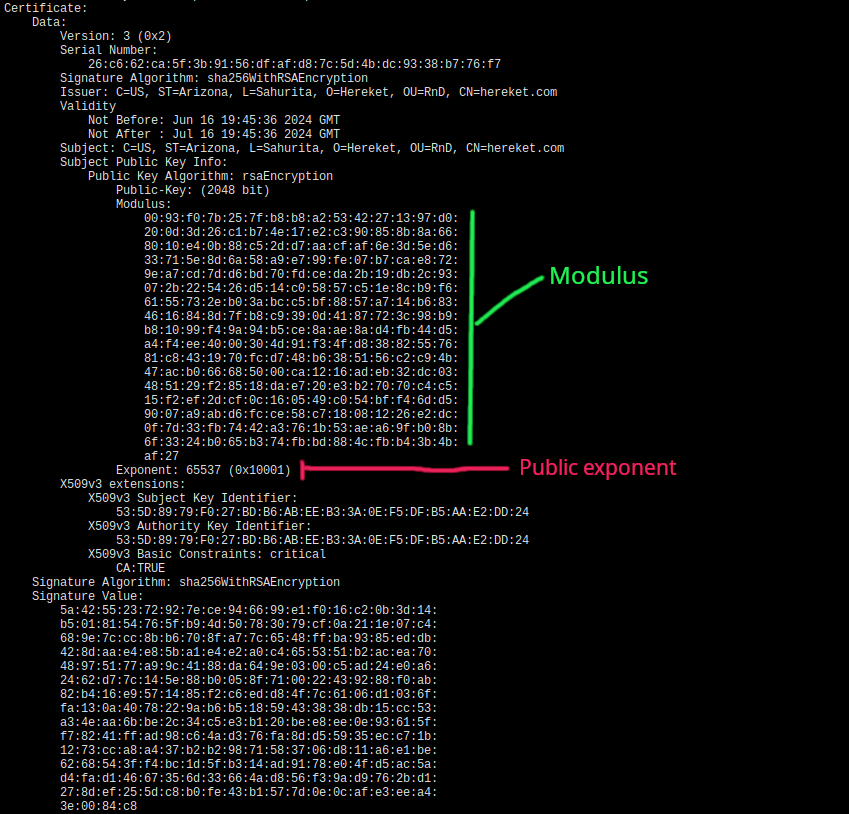
public.cert file will contain a bunch of information but somewhere in the middle it will have a public exponent and modulus. This is the file your browser downloads when you open a web page. You can get it with:

openssl x509 -in public.cert -noout -text

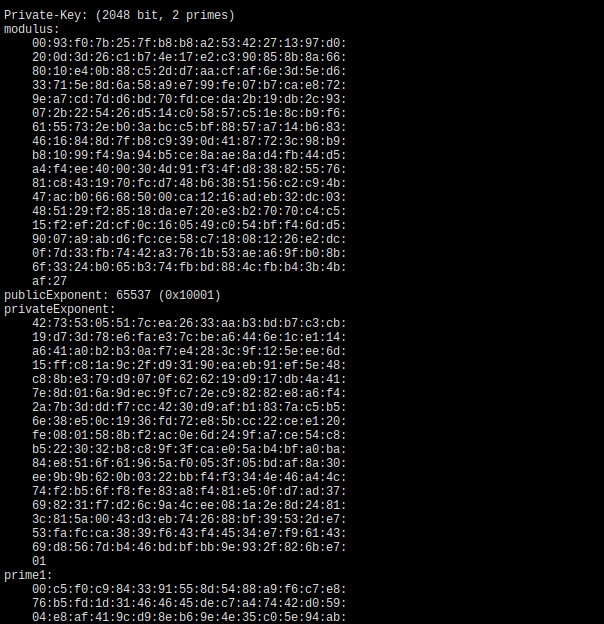
private.key file also contains a bunch of information including private exponent, public exponent and modulus. You can get it with:

openssl rsa -text -in private.key -noout

So browser (or other software) downloads a public certificate which contains public exponent and modulus (when RSA is used). With it encrypts some information which could be a key for AES and sends it to the server and server gets private exponent and modulus from its key file and decrypts it.

If you don’t want to bother with generating certificates and want to get just magic numbers for rsa you can use these commands:

openssl genrsa 2048 | openssl rsa -text -noout

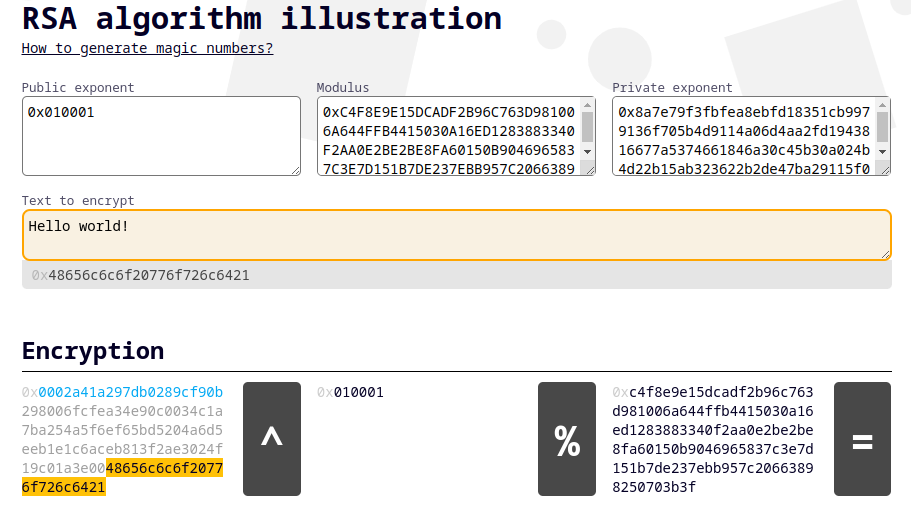
RSA toy

I create a simple toy to play around with encryption and decryption with RSA. You can check it out here: RSA toy. It includes ability to specify your own private and public keys with an exponent. Encryption is a bit slowerbut that is due to me not spending any time trying to optimize it and I hope it will not be too inconvenient.

Conclusion

RSA is still widely used algorithm for assymetric encryption and well worth the time looking into how it works. On top of that it is a good base and if you want to look into Diffie–Hellman next it will be very similar with just small changes.

In this post I wanted to try simplify learning RSA with examples, less math magic and some interactive examples to learn from.